
Команда "За СКОБКАМИ"
Сетевой проект "Тайны натурального ряда чисел"
Свойства, которыми обладает треугольник Паскаля.
Свойство №1.
Треугольник Паскаля бесконечен.
Свойство №2.
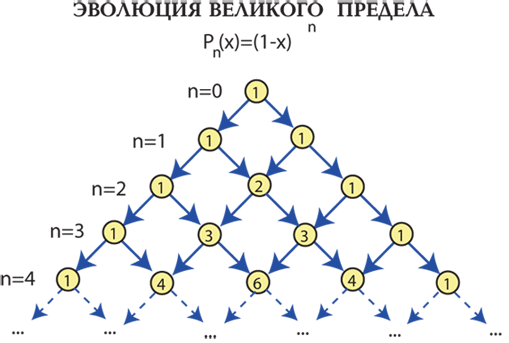
Сумма чисел в строках треугольника Паскаля равен 2 в степени n , где n - номер строки.
Свойство №3.
Треугольник Паскаля симметричен относительно центрального столбца.

Свойство №4.
Вторая диагональ треугольника Паскаля - это «треугольные» числа. Можно заметить, что если к 1 прибавить 2, мы получим 3, если к 3 прибавить 3, мы получим 6, а если к 6 прибавить 4 получится10, и таким образом каждый может продлить этот бесконечный ряд самостоятельно.

Свойство №5.
Первая диагональ треугольника Паскаля - это натуральные числа, расположенные по порядку.

Свойство №6.
Третья диагональ треугольника Паскаля - это «пирамидальные» числа или, более точно, тетраэдральные числа, показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).

Свойство №7.
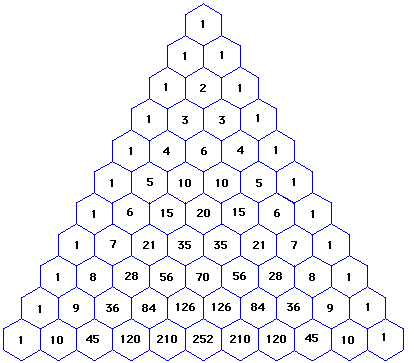
Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются).


Свойство №8.
Четвёртая диагональ треугольника Паскаля - это уже фигурные числа в четырехмерном измерении, поэтому это можно только представить в виртуальном мире.

Свойство №9.
В каждой строке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах.
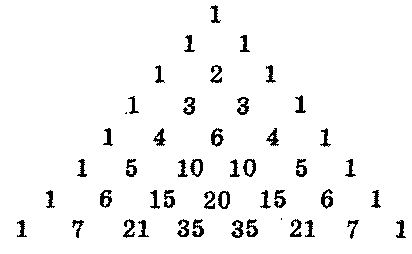
1+10+5=5+10+1
1+15+15+1=6+20+6
Свойство №10.
Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы)

Свойство №11.
Если номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число.

N=5
Числа 5, 10 делятся на 5
Свойство №12.
Если нечётное число в треугольнике Паскаля заменить на точки чёрного цвета, а чётные- белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники.

Свойство №13.
Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А.
