
Команда "За СКОБКАМИ"
Сетевой проект "Тайны натурального ряда чисел"
Вацлав Франциск Серпинский – известный математик польского происхождения. Является автором большого количества статей и книг. Серпинский оставил свой след в математике работами по теории множеств, аксиоме выбора, континуум-гипотезе, теории чисел, теории функций, а также топологии.
Вацлав Франциск Серпинский

Треугольник Серпинского
Треугольник Серпинского (иногда пишется Серпинский), также называемый прокладкой Серпинского или ситом Серпинского, представляет собой фрактал привлекательный фиксированный набор с общей формой равносторонний треугольник, разделенный рекурсивно на меньшие равносторонние треугольники. Первоначально построенный в виде кривой, это один из основных примеров самоподобных множеств, т. е. представляет собой математически сгенерированный узор, воспроизводимый при любом увеличении или уменьшении. Он назван в честь польского математика Вацлава Серпинского , но появился как декоративный узор много веков назад до работ Серпинского.
Удаление треугольников
Треугольник Серпинского может быть построен из равностороннего треугольника путем повторного удаления треугольных подмножеств:
-
Начните с равностороннего треугольника.
-
Разделите его на четыре равносторонних треугольника меньшего размера и удалите центральный треугольник.
-
Повторяйте шаг 2 до бесконечности с каждым из оставшихся меньших треугольников.
Каждый удаленный треугольник (трема) это топологически открытый набор . Этот процесс рекурсивного удаления треугольников является примером правила конечного подразделения .
Сжатие и дублирование
Та же самая последовательность фигур, сходящаяся к треугольнику Серпинского, может быть сгенерирована с помощью следующих шагов:
-
Начните с любого треугольника на плоскости. В каноническом треугольнике Серпинского используется равносторонний треугольник с основанием, параллельным горизонтальной оси (первое изображение).
-
Уменьшите треугольник до 1/2 высоты и 1/2 ширины, сделайте три копии и расположите три сжатых треугольника так, чтобы каждый треугольник касался двух других треугольников в углу (рисунок 1). Обратите внимание на появление центрального отверстия, потому что три усохших треугольника между ними могут покрывать только 3/4 площади оригинала. (Отверстия - важная особенность треугольника Серпинского.)
Повторите шаг 2 с каждым из меньших треугольников (рисунок 1 и т.д.)

Рисунок 1
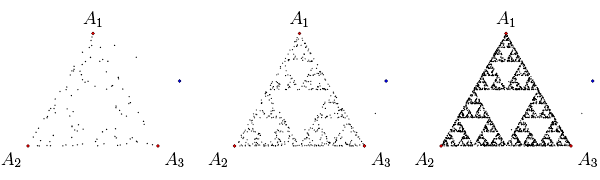
Игра хаос
-
Возьмите три точки в плоскости, чтобы сформировать треугольник, вам не нужно его рисовать.
-
Произвольно выберите любую точку внутри треугольника и примите ее текущее положение.
-
Случайно выберите любую из трех вершинных точек.
-
Переместитесь на половину расстояния от вашей текущей позиции до выбранной вершины.
-
Постройте текущую позицию.
-
Повторите, начиная с шага 3.
Интересные факты
-
Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные — в белый, то образуется треугольник Серпинского.
-
Изображения треугольника Серпинского в 1919 году стали мотивом нескольких графических произведений Георгия Нарбута, в частности эта фигура использована им при оформлении нескольких выпусков журнала «Мистецтво» (1919—1920 гг.).
-
Вариации фигур на основе треугольника Серпинского использованы в интерьере синагоги Бен-Эзра, Каир, Египет.
-
На основе треугольника Серпинского могут быть изготовлены многодиапазонные фрактальные антенны.
Четыре первых итерации фрактальных треугольников Серпинского использовались в орнаментах геометрической мозаики стиля косматеско в средневековых соборах Италии (начиная с XII века), арабских и персидских интерьерах.